直感を騙す確率のパラドックス「モンティ・ホール問題」

モンティ・ホール問題とは？

とある休日の昼下がり、陽だまりの落ちたソファでうたた寝をしていた父親は娘の遊び相手に抜擢されました。
「レイ」はパズルをしようと提案しましたが、「アリア」はおままごとをしたいと引き下がりません。

そう言うと、「アリア」はテーブルに３つの紙コップを逆さまに並べました。
それぞれの紙コップにはマジックでA,B,Cと書かれています。

「アリア」が言うには、３つの紙コップのどれか一つに当たりの書いた紙切れを入れたそうです。
「レイ」が当たりを引けばパズルで遊ぶ。はずれたらおままごとで遊ぶ。
なんとも分が悪いゲームですが、娘のことを溺愛している父親です。
「レイ」はかわいい娘のわがままだと簡単に受け入れました。

「レイ」はAの紙コップを選びました。
するとアリアは、しばらく黙ってから、ばつが悪そうにCの紙コップをテーブルからどけました。

真面目で優しい娘です。きっと、自分に有利なゲームにしたことに罪悪感を抱いたのでしょう。

さて、目の前にはAとB、ふたつの紙コップが残りました。
このとき、初めにAを選んでいた「レイ」は選択肢をBに変えた方が当たりの確立は高いのでしょうか？
それとも、選択肢を変えても変えなくても確率は変わらないのでしょうか？

選択肢はふたつ。当たりはひとつ。ならば当然、確率は二分の一。選択肢を変えても、変えなくても当たりの確率は同じ。

そう思いましたか？　まさに直感的には、そうなる人が多いかと思います。

しかし、実は確率は変わるんです。選択肢をAからBに変えた方が2倍も当たりの確率が上がります。

これが『モンティ・ホール問題』です。

どうして二分の一にならないのか？（『モンティ・ホール問題』の解説）

『モンティ・ホール問題』はアメリカのゲームショー番組で実際に行われていたゲームに由来する問題です。
司会者の名前がモンティ・ホールだったため、その名が名付けられました。

実際のゲームショーでは３つの扉の内、ひとつの当たりの扉を選ぶというゲームでした。

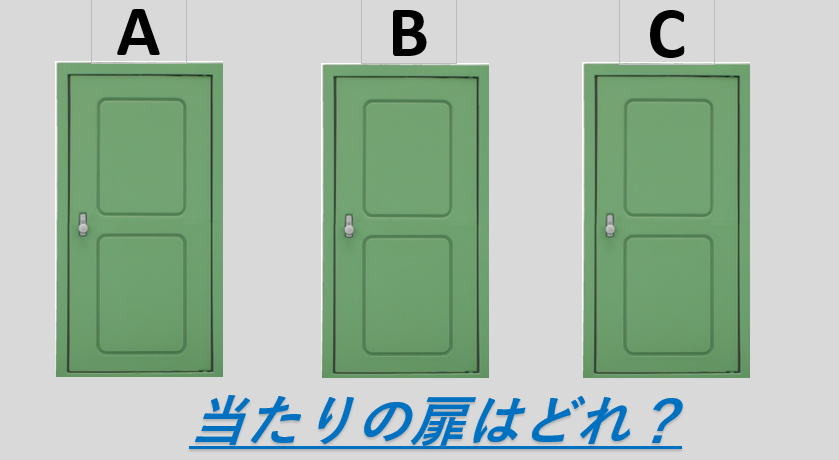
このゲームでは、プレイヤーがひとつの扉を選択したあとに、選ばれなかったふたつの扉の内から外れの扉がひとつ除外されます。

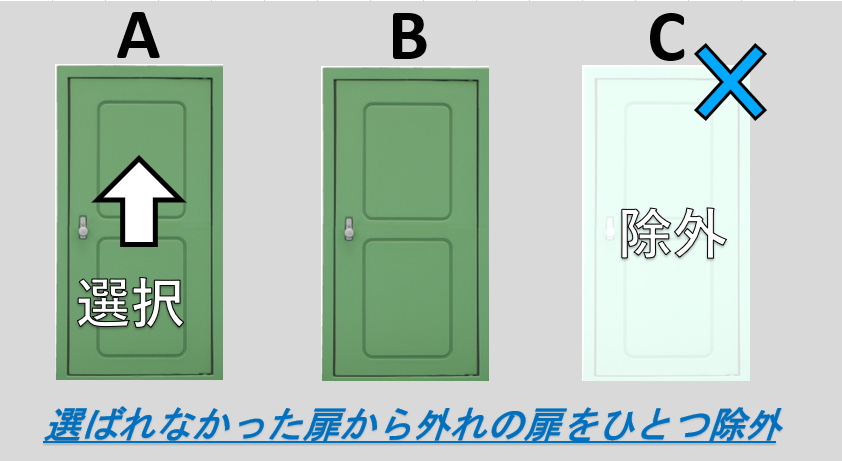
そして、プレイヤーは選択肢を変えてもよいと言われます。
このとき、選択をBに変えた方がいいのか？　というのが『モンティ・ホール問題』です。

■どうして二分の一の確率にならないのか？

ポイントは選ばれなかった扉から外れの扉が除外されるという前提があることです。

この大前提をもとに、最初に当たりを選んでいたときと、最初に外れを選んでいたときを場合分けして考えるとよく分かります。

・最初に当たりを選んでいた場合

最初の状況では三つの扉のうち、当たりは一つ。当たりを引く確率は1/3です。

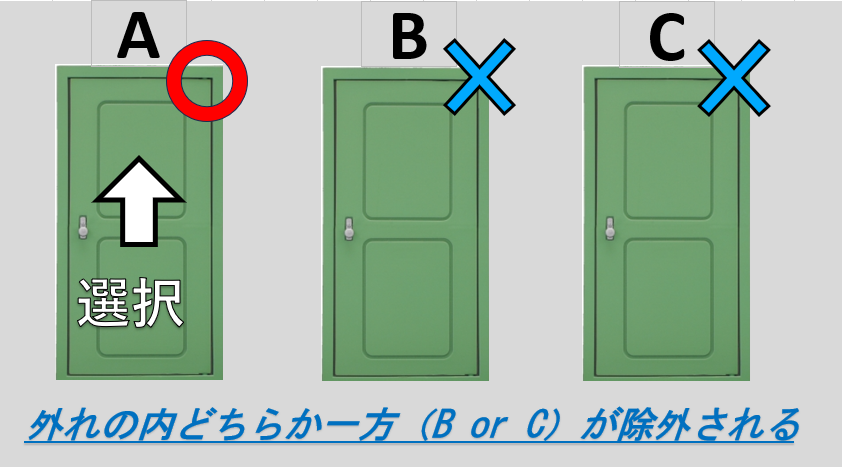
その後、外れの扉がひとつ除外されたあとに選択を変えると確実に外れます。

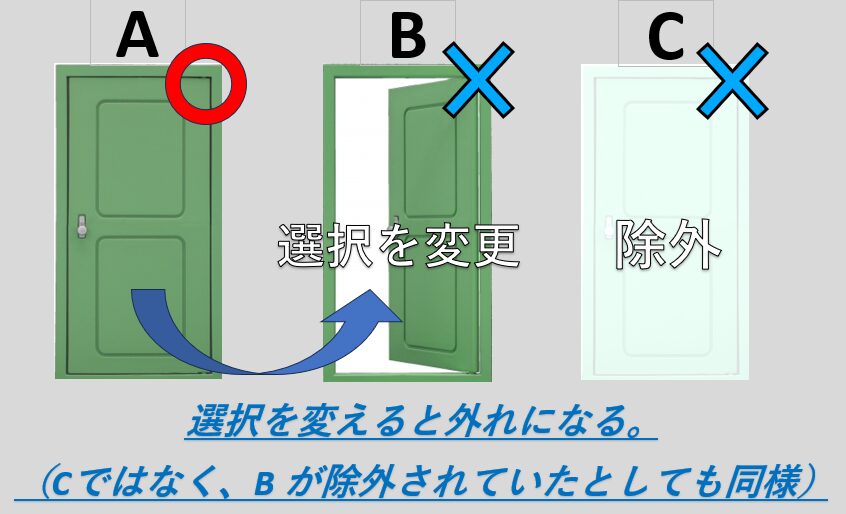
・最初に外れを選んでいた場合

最初の状況では三つの扉のうち、外れは二つ。外れを引く確率は2/3です。

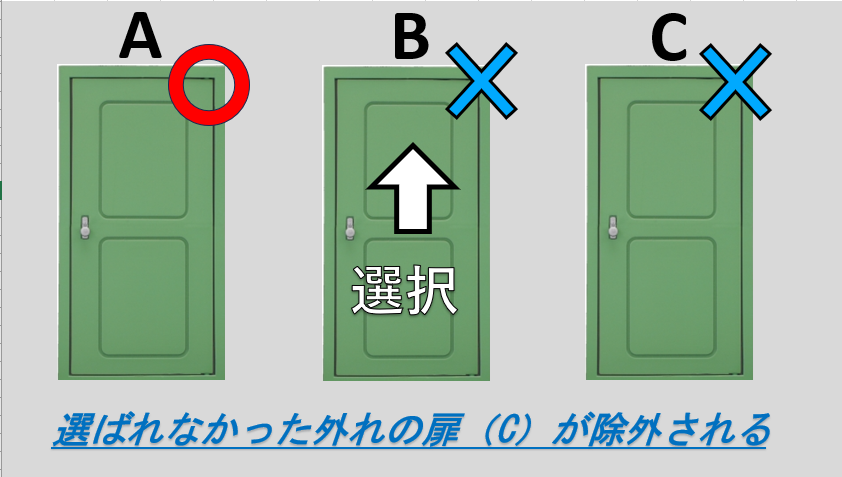
その後、選ばれなかった外れの扉が除外されるため、選択を変えると確実に当たります。

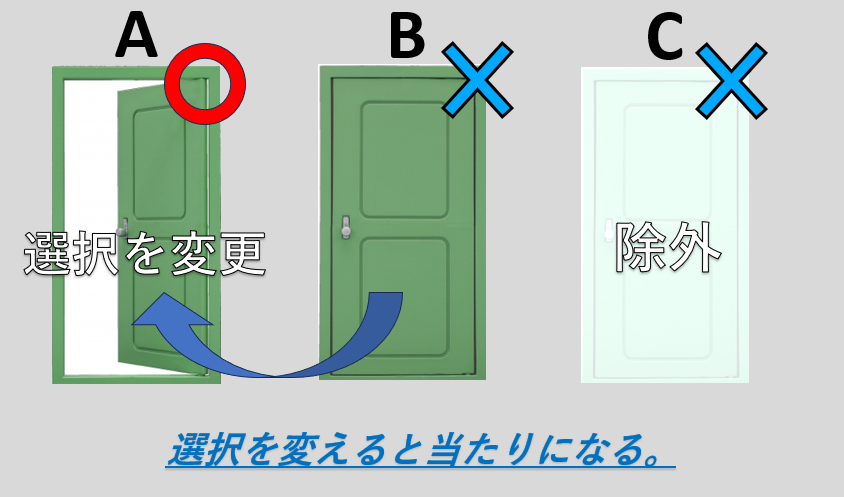
どうでしょう？
最初に当たりを選んでいたか、外れを選んでいたかによって、その後に選択肢を変えた結果は確定していることが分かると思います。
上の絵はAが正解の扉として扱いましたが、当たりがどの扉だろうと考え方は変わりません。

まとめると、

よって、このゲームでは外れがひとつ除外されたあとに、選択を変えた方が当たりの確率は高くなります。その確率は三分の二です。

以上が『モンティ・ホール問題』でした。

終わり